Matrix Multiplication in CUDA

In this post we dive a little bit deeper into CUDA and GPU parallelization with a more practical case: Matrix multiplication. Matrices are used everywhere, in convolutions, solving linear systems of equations, neural networks, transformers etc… And in every possible mathematics application you can think of, in physics, mechanics, computer vision etc. Therefore is interesting to be able to calculate matrix multplications as fast as possible, it’s a heavy compute calculation.

The code for this post is in my GitHub Blogging Code Repository in the cuda-matrix-multiplication subsection.

I thank Lambda AI for providing free credit to run the experiments described in the post. Throughout this post we will be using gpu_1x_a100_sxm4.

Matrix Multiplication

Consider we have two matrices $A_{M \times K}$ and $B_{K \times N}$ that mutiplied give a matrix $C_{M \times N}$. The first element of the size is the number of rows and the second the number of columns. Each element of the matrix $c_{i,j}$ is calculated as

\[c_{i,j}=\sum_{p=1}^{p=K}a_{i,p} \cdot b_{p,j}\]

So, per each element $c_{i,j}$ we perofrm $K$ multiplications and $K-1$ additions. Since there are $M \times N$ elements in the $C$ matrix, there will be a total of $M \times N \times K$ multiplications and $M \times N \times (K -1)$ additions. So we have a number of ploating points operations of approximately

\[\textbf{FLOPS} \approx 2 M \times N \times K\]

And the time complexity goes as

\[\mathcal{O}(M \times N \times K)\]

to simplify in our calculations we will consider squared matrices of size $N$, so time complexity will go as $\mathcal{O} (N^3)$ which is huge.

CPU implementation of matrix multiplication

We will use a very simple one threaded function that will be optimized by the compiler using the appropiate flags

void simpleMatrixMultiplication_cpp(const float* __restrict__ A,
    const float* __restrict__ B,
    float* __restrict__ C,
    const size_t M,
    const size_t K,
    const size_t N) {
    for (size_t i = 0; i < M; ++i) {
        for (size_t j = 0; j < N; ++j) {
            float sum = 0.0f;
            for (size_t k = 0; k < K; ++k) {
                sum += A[i * K + k] * B[k * N + j];
            }
            C[i * N + j] = sum;
        }
    }
}

In this it is implicit that the matrices are row-major, i.e. for row-column position $i$,$j$, the matrix element for $A$ is $a_{i,j}=A[j+i\times K]$. This is not the most performant code, it’s an example, if you want a better version of this multiplication do it with a library like LAPACKE like we did in the BLAS and LAPACK post.

GPU simple kernel

The most basic kernel for matrix multiplication is very similar to the CPU implementation above. We use two auxiliary variables row and col per thread to calculate the $C$ element per row and column.

__global__ void simpleMatrixMultiplication(const float* __restrict__ A,
    const float* __restrict__ B,
    float* __restrict__ C,
    const size_t M,
    const size_t K,
    const size_t N) {

    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;

    if (row < M && col < N) {
        float sum = 0.0f;
        for (int k = 0; k < K; ++k) {
            sum += A[row * K + k] * B[k * N + col];
        }
        C[row * N + col] = sum;
    }
}

This kernel serves our purposes to calculate the correct matrix multiplication but it can be improved a lot. For starters we aren’t using any __shared__ memory, this kind of memory is shared among all threads in a kernel and is much faster than the global memory. Here we are reading over and over from the global memory which makes this slow. We will fix this in the next kernel and comment other improvements.

GPU tiled multiplication

The following kernel makes use of the __shared__ memory to load elements of the matrix A and B so that they are faster to access by the individual threads of the block.

# define TILE 16
__global__ void tiledMultiply(const float* __restrict__ A, // M x K
                              const float* __restrict__ B, // K x N
                              float* __restrict__ C,       // M x N
                              std::size_t M,
                              std::size_t K,
                              std::size_t N) {

    int by = blockIdx.y;
    int bx = blockIdx.x;

    int ty = threadIdx.y;
    int tx = threadIdx.x;

    // global row/col this thread is responsible for
    int i = by * TILE + ty;  // row in C
    int j = bx * TILE + tx;  // col in C

    __shared__ float As[TILE][TILE];
    __shared__ float Bs[TILE][TILE];

    float value = 0.0f;

    // number of tiles along K
    int numTiles = (K + TILE - 1) / TILE;

    for (int ph = 0; ph < numTiles; ++ph) {
        // column in A, row in B that this thread wants to load
        int aCol = ph * TILE + tx;  // along K
        int bRow = ph * TILE + ty;  // along K

        // load A tile (row = i, col = aCol)
        if (i < M && aCol < K)
            As[ty][tx] = A[i * K + aCol];
        else
            As[ty][tx] = 0.0f;

        // load B tile (row = bRow, col = j)
        if (bRow < K && j < N)
            Bs[ty][tx] = B[bRow * N + j];
        else
            Bs[ty][tx] = 0.0f;

        // sync all threads to make sure the tiles are loaded
        __syncthreads();

        #pragma unroll
        for (int t = 0; t < TILE; ++t) {
            value += As[ty][t] * Bs[t][tx];
        }

        // sync before loading the next tile
        __syncthreads();
    }

    // write back only if in-bounds
    if (i < (int)M && j < (int)N) {
        C[i * N + j] = value;
    }
}

That we launch with a C++ function wrapper

void tiledMultiply_call(const float* __restrict__ A,
                    const float* __restrict__ B,
                    float* __restrict__ C,
                    std::size_t M,
                    std::size_t K,
                    std::size_t N){
    dim3 threads(TILE, TILE);
    dim3 blocks((N + TILE - 1) / TILE, (M + TILE - 1) / TILE);
    tiledMultiply<<<blocks, threads>>>(A, B, C, M, K, N);
    cudaDeviceSynchronize();
}

Let’s understand this code, an exellent visual representation of the calculation here is found in this YouTube video. For a detailed explanation check the book Programming Massively Parallel Processors.

In matrix multiplication we find that we use the same matrix elements from A and B over and over so the idea is to move those elements to the shared memory to use them in small tiles. Shared memory is much faster than global memory and since by doing this we are reducing the number of calls, it will most certainly reduce our total calculation time.

In the kernel tiledMultiply we focus on calculating the elements of C for a tile of size TILE for each block. Think of defining your blocks so that they cover all the elements in matrix C. In the code we calculate how many tiles we need, since the mutliplication dimension is K (columns of A and rows of B), we need K tiles per block (or, to cover all the elemtns in case K is not divisible by TILE we calculate (K + TILE - 1) / TILE). Then for every tile we load the elements of A and B that will participate in the multiplication, inside that same for loop we sync for all threads in that block. Indeed!, inside your for loop you can stop till all threads load their data, then you just need to multiply as usual the elements of the matrix A and B to give you the individual summands before syncing threads again and finally assigning the value for the element i * N + j.

When launching this kernel we consider squared blocks of size TILE x TILE, usually this tile is of size 16, remember the shared memory is quite limited on GPUs. Then we need to launch a total of (N + TILE - 1) / TILE blocks in the x dimension (rows) and (M + TILE - 1) / TILE in the y drection, columns to cover all elements of C. This is conveniently wrapped in the function tiledMultiply_call.

Matrix multiplication performance

So far we went very deep into the coding. Let’s calculate some benchmarks. To execute this part go to the cuda-matrix-multiplication and compile and execute the code with

./scripts/build.sh
./scripts/execute.sh

This will produce a csv that can then be analyzed in Python. To produce the plots just install the python environment and run the analysis script:

./scripts/install_env.sh
.venv/bin/python scripts/analyze.py

The first graph shows the time taken to multiply two squared matrices of size $N$. The green line corresponds to the GPU while the black line to the CPU.

Figure 1. GPU vs CPU calculation time comparison as a function on the matrix size for square matrices of size $N$. For GPU we include the loading time, calculation time and loading back to host times.

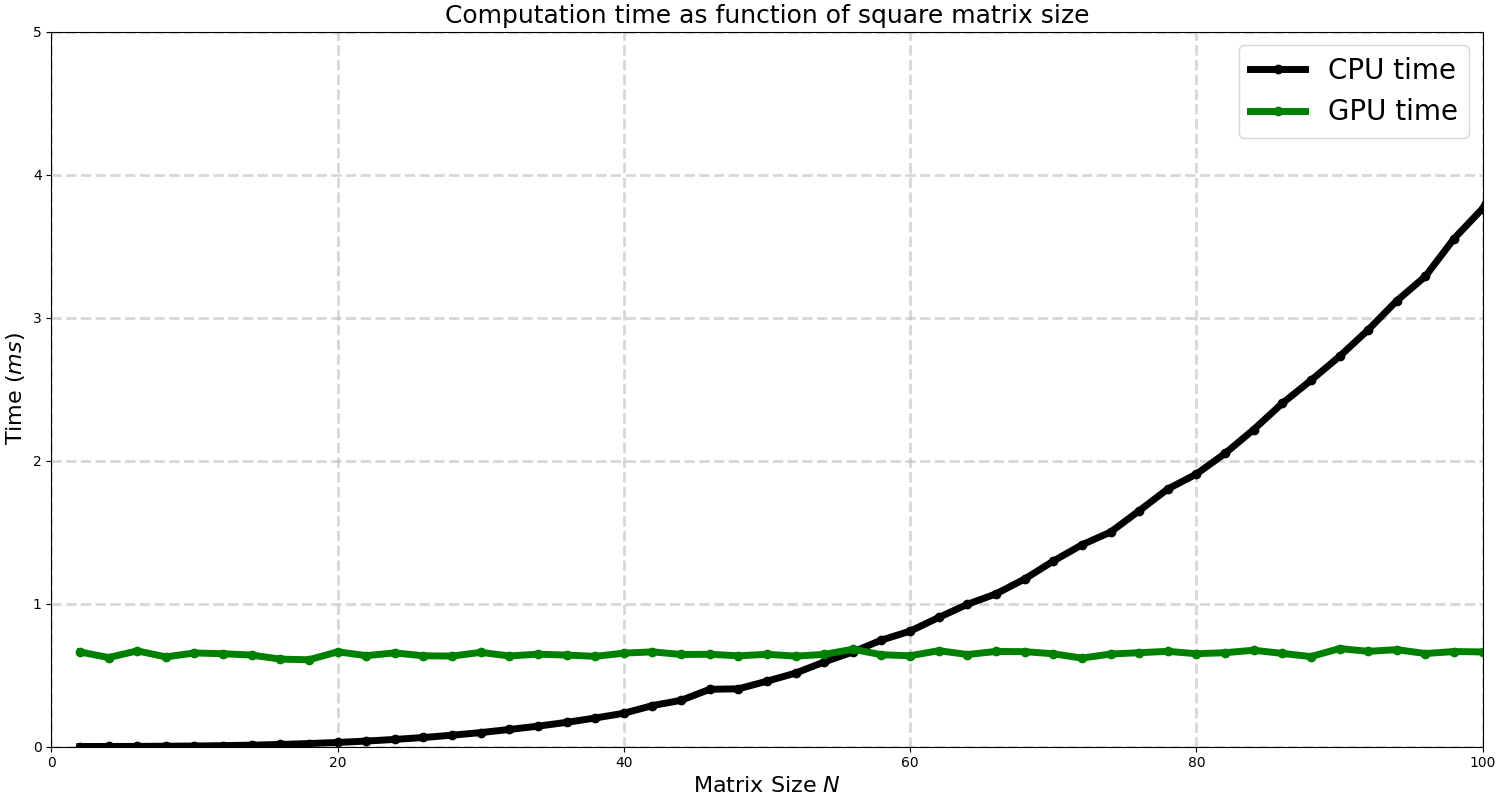
We can see how in small matrices the time taken is constant (independent of the size of the matrix) because the majority of the time is spent initializing the process and loading the data. CPU in smaller matrix sizes is much faster. For matrices smaller than $N=55$ it is better to use CPU whilst GPU is faster. For larger matrix sizes we make the following plot:

Figure 2. Same as Fig. 1 but with larger matrix sizes

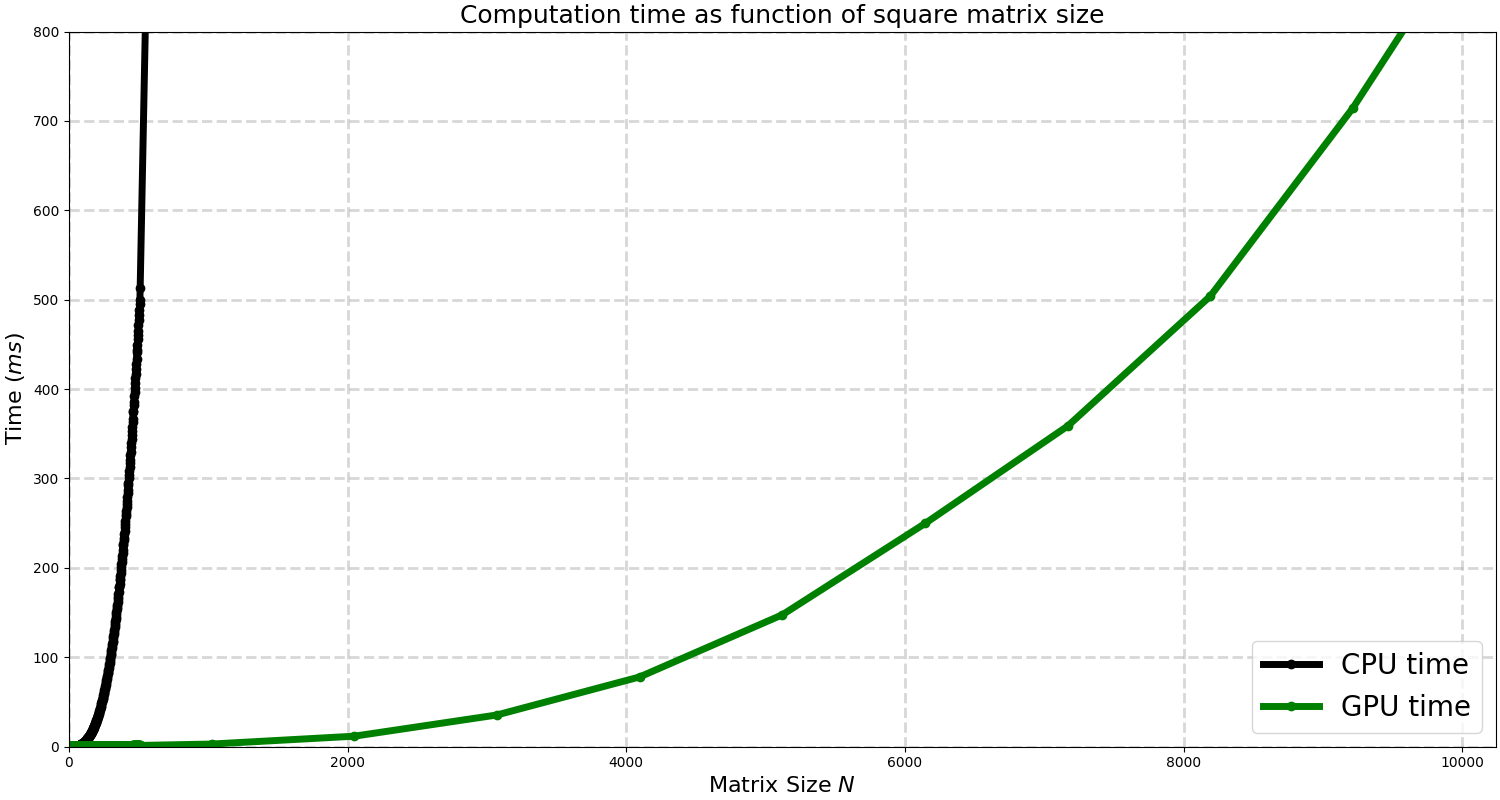
It can be seen that CPU time goes out of the scale whilst GPU slowly increases. For $N \approx 10K$ elements the multiplication time is around 0.85 seconds for the GPU.

So far we have just considered the slow approach for the GPU, the one that loads the elements from the global memory in the GPU. Still we get huge speedups compared to CPU. In the following plot we compare three methods of matrix multiplication: The simple approach, the tiled matrix multiplication and finally using a library in CUDA called cuBLAS, the CUDA equivalent of BLAS.

Figure 3. Matrix multiplication times for two squared matrices as a function of the matrix size. The green line corresponds to the simple matrix multiplication (the same as in Fig. 1 and Fig. 2). The blue line our custom tiled matrix multiplcation implementation and the gray line the cuBLAS implementation.

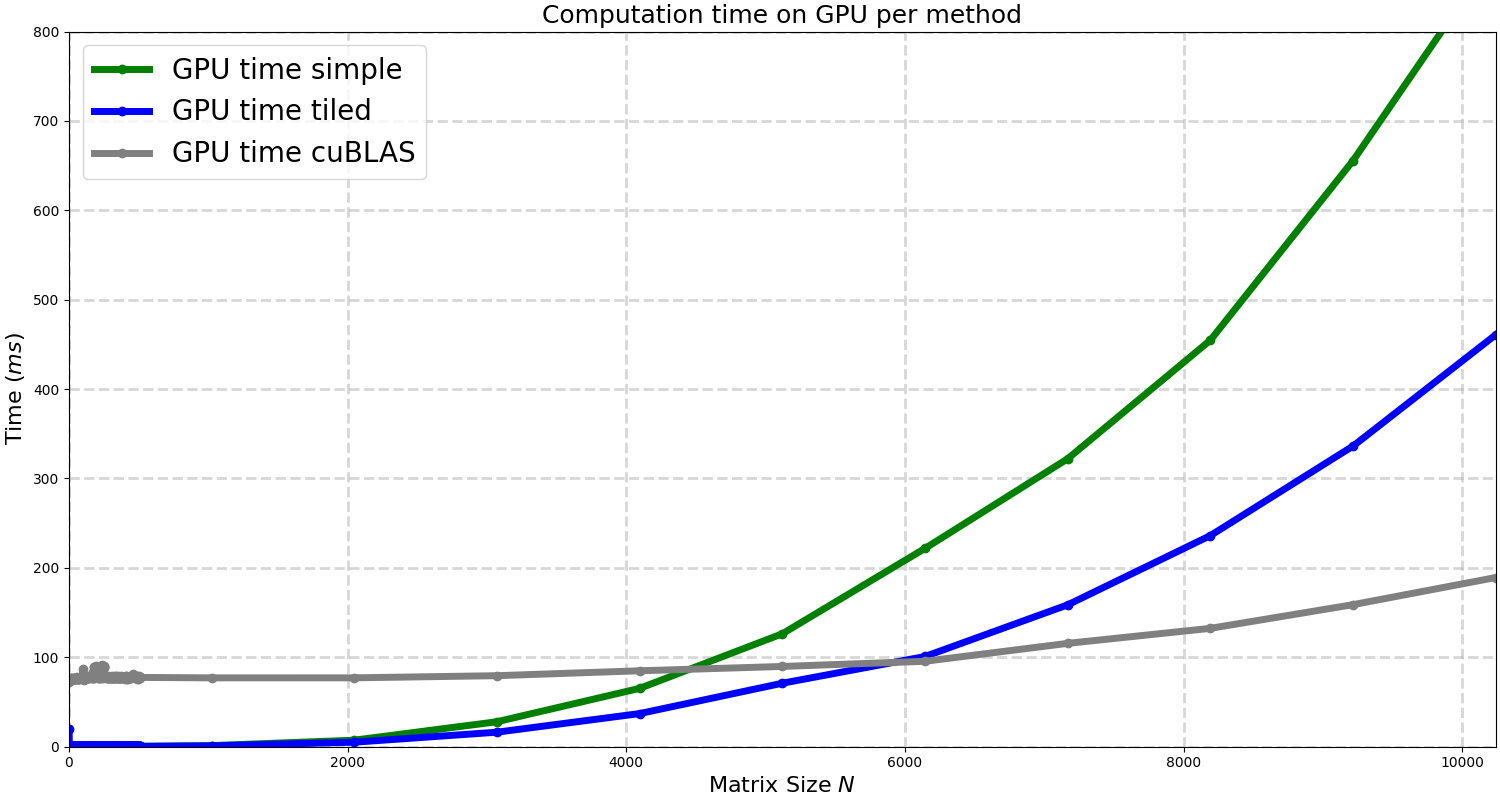
Our tiled matrix multiplication clearly improves the simple one initially considered. The improvement seems to be around 2X the time. However the cuBLAS implementation is much faster, around 4x, which is impressive. cuBLAS has decades of optimization so it is expected to run much faster than any custom implementation.

cuBLAS uses specialized matrix mutiplication hardware, tensor cores. Those can give up to 8-16x more FLOPs than standard FP32 cores used in our custom implementation. Also cuBLAS has deeper tiling, it uses large block tiles and each thread computes multiple elements. These are the main optimizations but we can list more and will probably take another entire post to describe them all.

This last graph shows us that as expected it is better to use the library cuBLAS to multiply any two matrices on the GPU. However, the call for these functions has a cost, you cannot implement something custom i.e. a matrix multiplication and another custom optimization operation using a self programmed kernel. The moment you want to fuse operations in kernels you would probably need to implement your own multiplication with other operations inside the same CUDA kernel.

Conclusions

We have seen how to multiply two matrices in CUDA. Specifically we learned how to use the shared memory to gain some extra speedup in the GPU. Finally we showed that experience is a plus and using cuBLAS is the easiest route to get a super optimized matrix multiplication. Do not reinvent the wheel and try to implement your version of CUDA matrix multiplication unless you need it for a very specific application that involves fusing kernels with other custom operations.