Nvidia-GPU Performance
GPUs or Graphical Processing Units have become essential in high performance computing these days. They are efficient hardware that can parallelize small calculations. For instance, in Machine Learning (ML) and Artificial Intelligence (AI), GPUs are ubiquitous, as almost all operations are matrix multiplications, convolutions, max pooling… Operations that can be paralellized easily. However, GPUs are not suitable for any kind of calculation, in this post we will understand when it pays off to bring the calculation to GPU for a very simple example.
I thank Lambda AI for providing free credit to run the experiments described in the post. Throughout this post we will be using gpu_1x_a100_sxm4, an Ampere 100 GPU, the same as used in the post CUDA Utils. As always the code can be found in my github repository.
The problem
Given two arrays of floats of length N, their sum m times. This is, for each element a in $\vec{a}$ and each element b of vector $\vec{b}$ we make the sum m times. A total of $N \times m$ floating point sums. We can write the CPU code in C++ as
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// Create host a, b, c
std::vector<float> h_a(N), h_b(N), h_c_cpu(N);
// Fill a and b with random floats 0 to 1
for (int i = 0; i < N; ++i) {
h_a[i] = static_cast<float>(std::rand()) / RAND_MAX;
h_b[i] = static_cast<float>(std::rand()) / RAND_MAX;
}
// Sum each element of the arrays i...N, a total of m times
for (int i = 0; i < N; ++i) {
double acc = 0;
double s = h_a[i] + h_b[i];
for (int j = 0; j < m-1; ++j) {
acc = acc + s;
}
h_c_cpu[i] = acc;
}
I agree the code seems a bit useless, why don’t we do…
1
double s = (h_a[i] + h_b[1]) * m;
So that it would be only N additions?. We want to explicitely make the sum m times per array element. Also we want to avoid adding constants to this loop, e.g. acc = acc + 1. That would make the compiler to optimize the code and run much faster, the point of this calculation is to perform m sums for each array element.
GPU kernel for vector addition
This is one of the simplests CUDA kernels one can write, but before starting to explain it, if you are new into CUDA programming, please take a look at the CUDA programming model. Make sure you understand what is a thread, a block and a grid. A good visualization of the model can be found here. Another great resource is Programming Massively Parallel Processors: A Hands-on Approach, this is my reference book for GPU programming.
Our CUDA kernel for addition of two vectors hould look like this:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template<typename T>
__global__ void vectorAdd(
const T* __restrict__ a, // vector a
const T* __restrict__ b, // vector b
T* __restrict__ c, // vector c
int n, // number of elements of a, b, c
int m=1) // number of additions
{
int idx = blockDim.x * blockIdx.x + threadIdx.x;
if (idx >= n) return;
T s = a[idx] + b[idx];
T acc = T(0);
for (int j = 0; j < m-1; ++j) {
acc = acc + s;
}
c[idx] = acc;
}
We define a template to adapt in case we want to test for other types like int or double instead of float. Every CUDA kernel has to start with __global__, that tells the nvcc (the compiler) that this is code to be executed at the GPU. Then, inside the function we have the global index of the thread, idx. We will launch 1D blocks in one grid so we are working only with the x dimension, in this case the idx can be written as the block dimension times the block index plus the thread index within the block, blockDim.x * blockIdx.x + threadIdx.x;. Then we have the conditional on the global thread index, a condition that, even though not mandatory, it is very recommended to add; the index cannot exeed the total number of elements of the array. If the thread is larger, no worries, we just don’t do anything and we leave the function for that thread. Finally we have the sum $m$ times.
To launch this kernel on any C++ file I normally write a wrapper C++ function:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<typename T>
void vectorAdd_wrapper(
const T* __restrict__ d_a,
const T* __restrict__ d_b,
T* __restrict__ d_c,
int N,
int m,
int ThreadsPerBlock){
int blocksPerGrid = (N + ThreadsPerBlock - 1) / ThreadsPerBlock;
vectorAdd<<<blocksPerGrid, ThreadsPerBlock>>>(d_a, d_b, d_c, N, m);
CHECK_LAST_CUDA_ERROR();
CHECK_CUDA_ERROR(cudaDeviceSynchronize());
}
Here I specify how many ThreadsPerBlock to use and therefore infer the blocks needed to run my addition, Then launch the kernel and check the errors with CHECK_LAST_CUDA_ERROR (checks last errors in the kernel launch) and CHECK_CUDA_ERROR (checks error outputs from functions that return the type cudaError_t, for instance cudaDeviceSynchronize). Using these two cuda error functions is a good pattern to actively catch every error that can be happening in your GPU.
CPU vs GPU in vector addition
With all this and the code in the github repository we can start calculating vector additions in the GPU and compare them to the CPU. First let’s calculate how much time does it take to calculate the addition of two vectors as a function of ttheir size $N$.
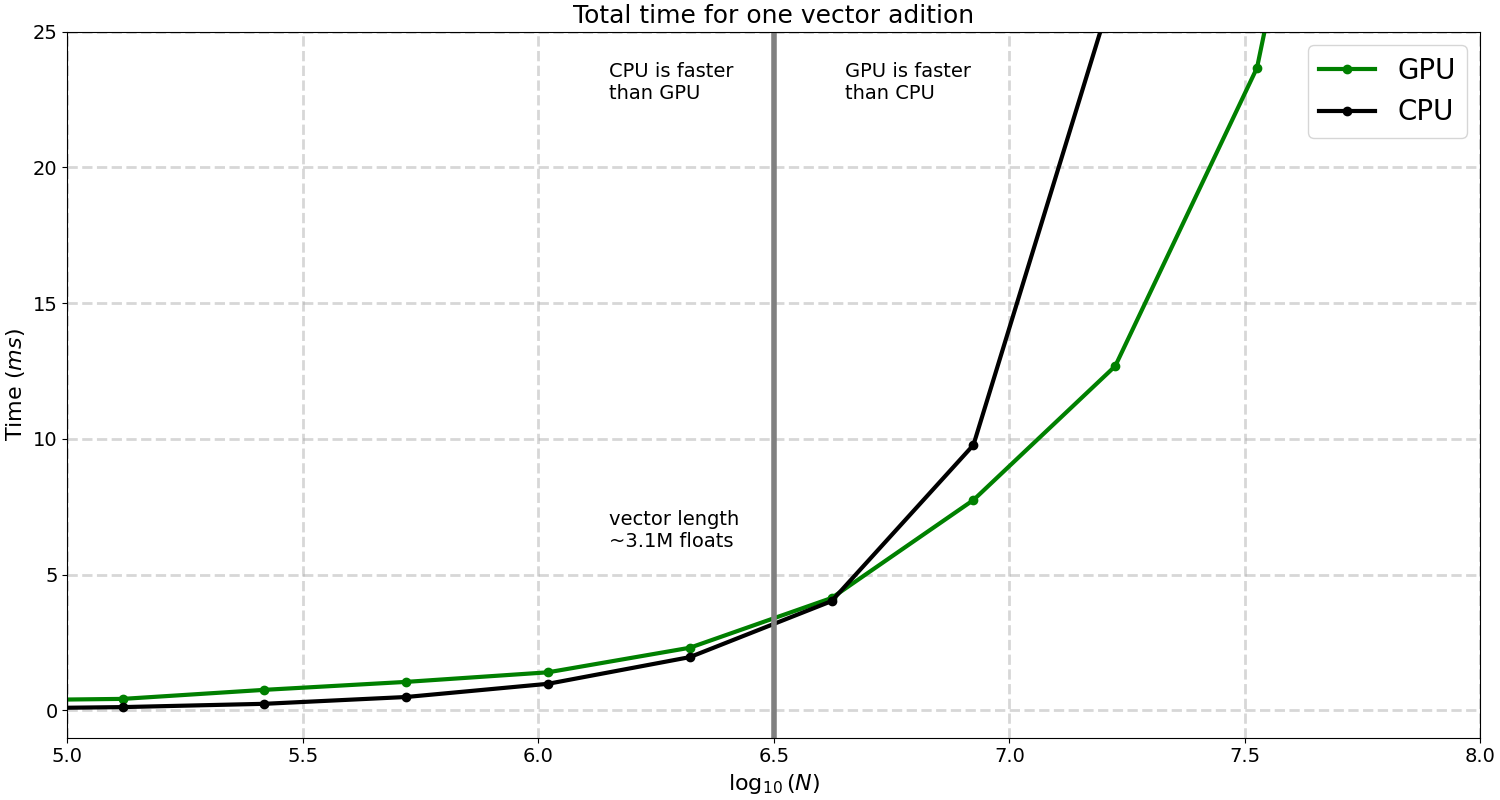
The first we notice is that for values smaller than $\log_{10}N$ smaller than ~6.5 the CPU is faster. That may be surprising if you are new in the GPU world. How can it be that the CPU is faster in a parallel task?. Well, there’s two reasons, first, there is an overhead of allocating memory in the GPU, then transfer data, moving the data back to the CPU and free the memory in the GPU, that’s a lot of steps. Also another reason is that a CPU is in general faster than the GPU individual thread. As $N$ grows we see that the GPU calculation time becomes smaller than the CPU, at this regime is where it pays off (computationally speaking) to use the GPU.
But he above calculation is only for one addition, what if we do $m$ additions once the data is uploaed to the GPU?.
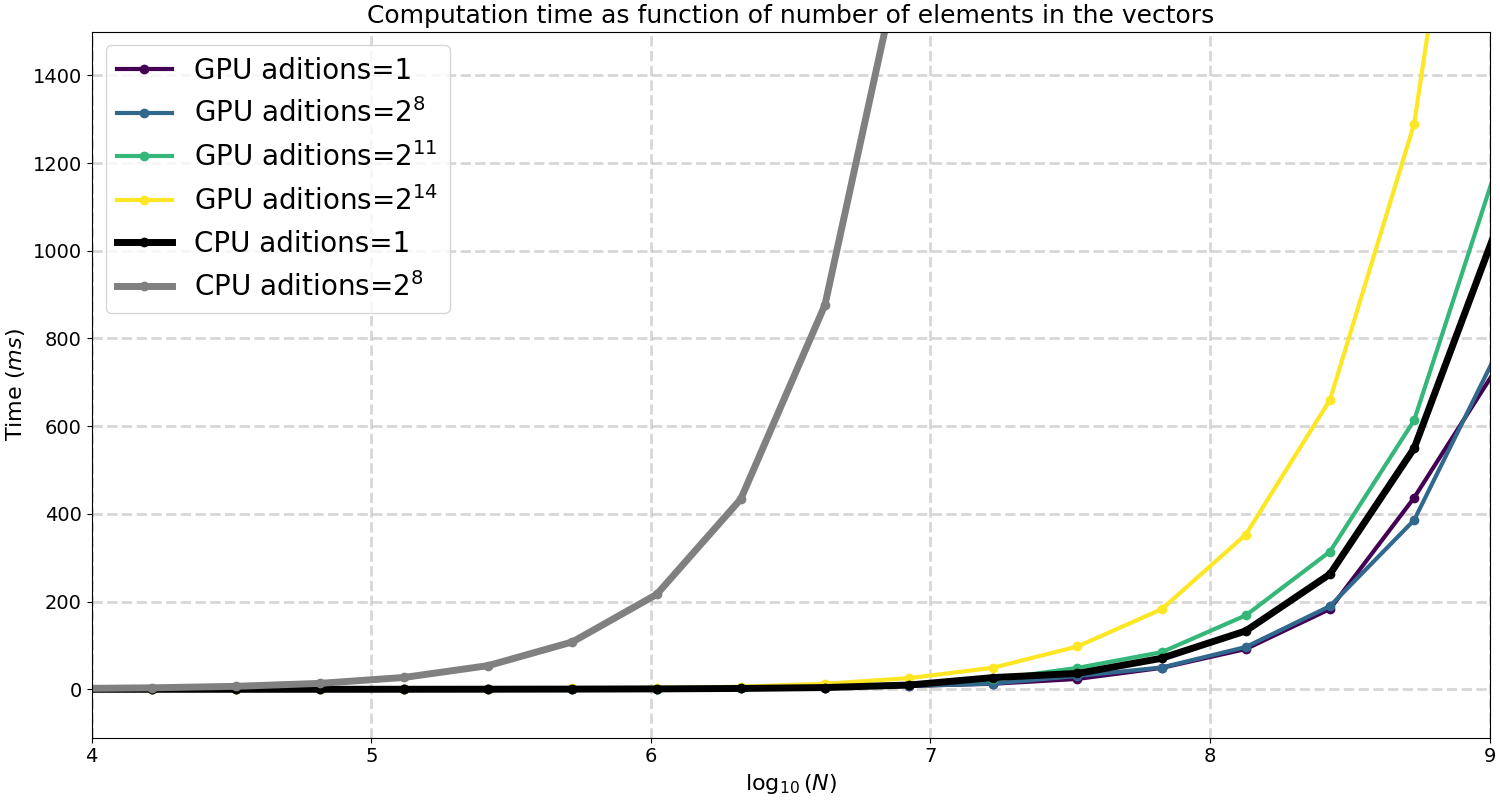
In this figure you can see that the CPU for 1 addition and $2^8$ are very different, the latter is much more lenghtly. And this is expected, if we compare the same GPU additions we see that the curves are much closer, i.e. the fact that we parallelized the calculation makes it almost equal in time in the GPU. As we look at higher numer of additions this curve increases in time (see yelllow curve for $2^{14}) but it is impressive that the time difference is not that large.
From the above we can already say something (rather obvious) about GPUs, if your calculation can be parallelized and has a lot of operations it probably pays off to bring it to the GPU.
GPU times
It’s time to dive deeper into the total time of the GPU. As mentioned before there are 5 times that contribute to the GPU calculation time
- Allocation
- Data transfer from host to device
- Calculation
- Data transfer from device to host
- Free memory
We can look into this in the following graph
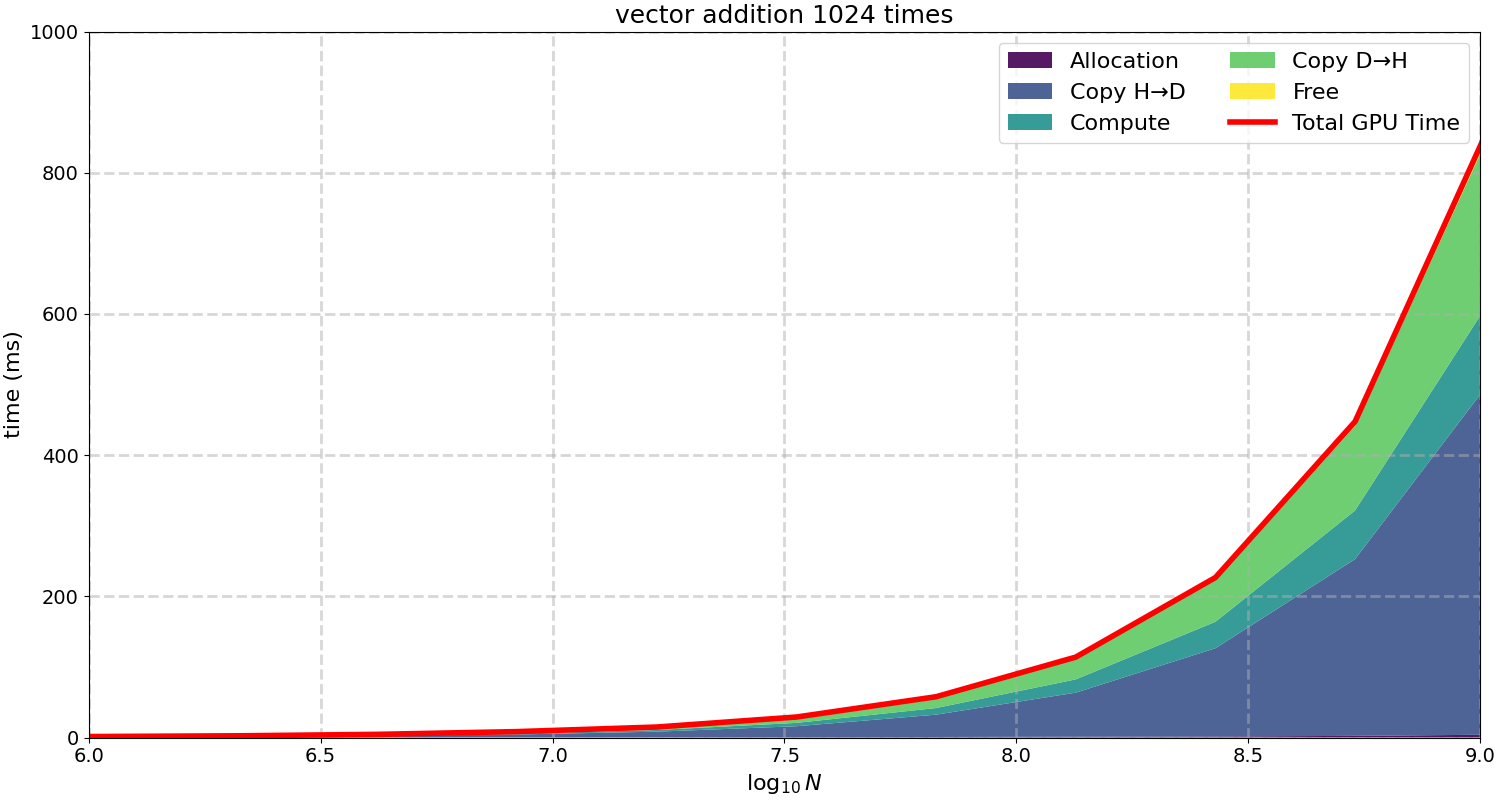
Here we show in colors all the times including the total GPU time in a cummulative way. The allocation time seems inexistent and indeed it is very small compared to the rest, that is only if we have done a previous allocation in the GPU, the initial allocation always takes a significant amount of time. I have preallocated memory before allocating the bytes needed at every step in the graph. The copy time increases as $N$ increases. That is logical, we are trasnfering bigger vectors into the GPU. Also the compute time increases, and this could be surprising, after all each trhead in the GPU calculates the same ammount of additions, 1024. However if the number of elements in the vector is very large we may be batching our calculations, i.e. first we calculate $K$ vector elements, then the next $K$… in sequence. That may be increasing the total time for the calculation. Here we just fixed the blocks per thread to 512. After the calculation we have to copy back the data from the GPU to the host, if you notice, that takes less time that from the host to the GPU, the reason is that when copying from CPU to GPU we need to copy $a$ and $b$ vectors, whereas from GPU to CPU we only copy the result, $c$, that’s half of the bytes, therefore approximately half of the time. Finally freeing the memory is almost unnoticeable when the vector size is large.
Let’s compare the explicit times for 2048 additions at a small and large vector size:
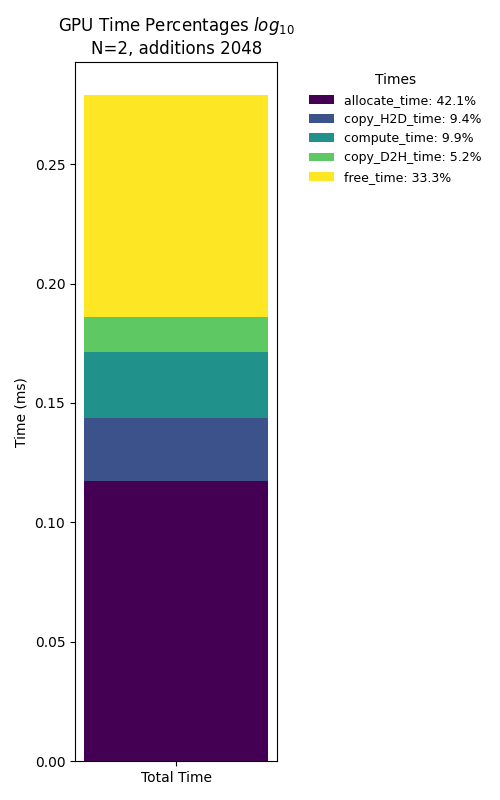
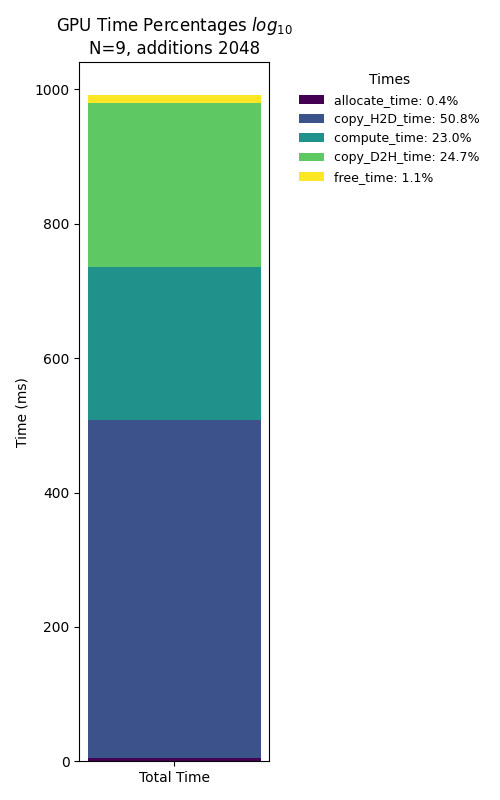
In the limit of small vector size the time that it takes to allocate and deallocate the memory and transfer the data from host to device is large compared to the calculation. At this limit is clearly not worth it to use the GPU. For large vector sizes the percentage of the compute time increases, and that is what we want when using a GPU, to maximize the time of actual calculation with respect to allocation and data transfer.
But something interesing happens here: By design of our kernels each thread computes $m$ additions, if we launch all threads in parallel there is a limit of them so internally the GPU launches the calculations in batches. To be more specific, the GPU has finite number of Streaming Multipcoressors (SMs), and a finite number of cores per SM. So the time increase in this particular calculation is actually expected to be linear (as we see in Figure 3 noticing that the scale is logarithmic).
Takeaways
GPUs are great but they aren’t free lunch. In some cases they may make your calculation slower than using a GPU. The vector adition example is very basic, but it’s useful to get some general guidelines when coding in CUDA
- Keep data ransfer between host and device (GPU) the minimum possible.
- Use multiple threads per block without exeeding the maximum of the indications (usually 1024 threads per block)
- Use the GPU to make many operations, many operations per thread.
GPU optimization is a large topic that we can’t cover entirely in this post, but Nvidia already compiled a Nvidia CUDA-C programming guide. Some fo the highlights are:
- Use memory hierarchy: There are different levels of memory from Global, shared, registers and constant memory.
- Use asynchronous operatiosn: It’s possible to overlap data transfer between host and device at the same time that the GPU is executing kernels. We can do that with streams.
- Avoid excessive branching in threads. Threads executed in parallel (known as warps) should take more or less the same amount of time, otherwise the calculation time increases to the worst performer.
- Keep threads busy at all times, optimize so that threads have available data to calculate.
Hope you enjoyed this very simple CUDA demonstration. There’s going to be more on CUDA soon!.