Prime Numbers
Prime numbers are the building blocks of arithmetics. In this short post we will investigate some attributes of prime numbers and how to work with them in a computer.
One of the main applications of prime numbers is in some algorithms related to cryptography (e.g. RSA) and therefore it is related to techniques developed for privacy preserving machine learning. In a previous post we have defined groups and fields using prime numbers and our main aim in this post is to show how to calculate prime numbers and check whether a certain number is prime or not. Due to the mathematical importance of primes I considered worthwhile to write a full post about them. A prime number is a natural number that is only divisible by himself and 1. For instance 7 is a prime number because there’s no natural number smaller than 7 that divided by 7 results in an integer. Some sorted prime numbers are \(2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, \cdots\).
The building blocks of arithmetics
Prime numbers are considered the building blocks of arithmetics because no matter what natural number you may think of, you can express it as product of prime numbers. For instance, take \(30\), it can be decomposed as \(2·3·5\). Or \(123456\) in \(2^6·3·643\). The process of decomposing a number to its prime number factors is called it factorisation. The fundamental theorem of arithmetics (a.k.a unique factorisation theorem) states that every integer greater than 1 either is a prime number itself or can be represented as the product of prime numbers and furthermore this representation is unique. So given an arbitrary integer a we can write it as
\[\begin{equation} a=p_1^{e_1} \cdot p_2^{e_2} \cdots p_r^{e_r} \end{equation}\]where the p’s are prime numbers and e’s are the exponentiation of those.
But let’s get back to topic, we are interested in cryptography, what does all this have to do with it?. Well, in modern cryptography one tries to find hard mathematical problems to solve that are easy to check. Factorisation of prime numbers is a very difficult task to solve. There are algorithms like Pollard’s factorisation or Lenstra elliptic-curve factorisation that are efficient but if you have a quantum computer at hand the best by far is the Shor algorithm (it is polynomial in log(N)). In RSA algorithm one chooses two large prime numbers $p$ and $q$ and compute $N=p \cdot q$, the task of the adversary to break the code is to find the factors of $N$. For sufficiently large prime numbers the probability of solving this task by chance is negligible and the classic factorisation methods take too long so in practice it is impossible to crack in today’s computing power based on binary operations. Conversely having $p$ and $N$ it is very easy to check if $p$ is a factor of $N$ with one operation. This is also a requirement to modern crypto protocols.
How many prime numbers are there? Can we find a “magic formula” to get them all?
It was proven by Euclid back in 300 BCE that there are infinitely many prime numbers. The largest one found as of August 2020 is 2^82589933-1 and has 24,862,048 digits when written in base 10.
It would be nice to have a formula that when you input “give me the 532 prime” it would output 3833 (the 532th prime), all that taking O(1) compute time. Unfortunately this formula does not exist and finding new prime numbers take a lot of computational effort. That means that they are not predictable and this is one of the mysteries on primes… once you see a prime you don’t know when you’ll find the next one. Is there some kind of random/chaos in prime number structure? Nobody knows yet.
Even though we can’t predict primes with a formula we can calculate the probability of finding a prime number in between a range of numbers. We define $\pi (x)$ as the number of prime numbers smaller than $x$. For instance, $\pi (20)=8$, because prime numbers smaller than $20$ are $2, 3, 5, 7, 11, 13, 17, 19$. Therefore, to calculate the number of primes between $x_2$ and $x_1$ ($x_2$>$x_1$) we just need to subtract both $\pi (x_2)-\pi (x_1)$. Here $\pi (x)$ is exact calculation and we have to do it numerically. The prime number theorem establishes the asymptotic distribution of prime numbers by approximating the count to $x/\ln(x)$
\[\lim_{x \rightarrow \infty} \frac{\pi (x)}{x/\ln(x)}=1\]A graphical representation of this result is shown below
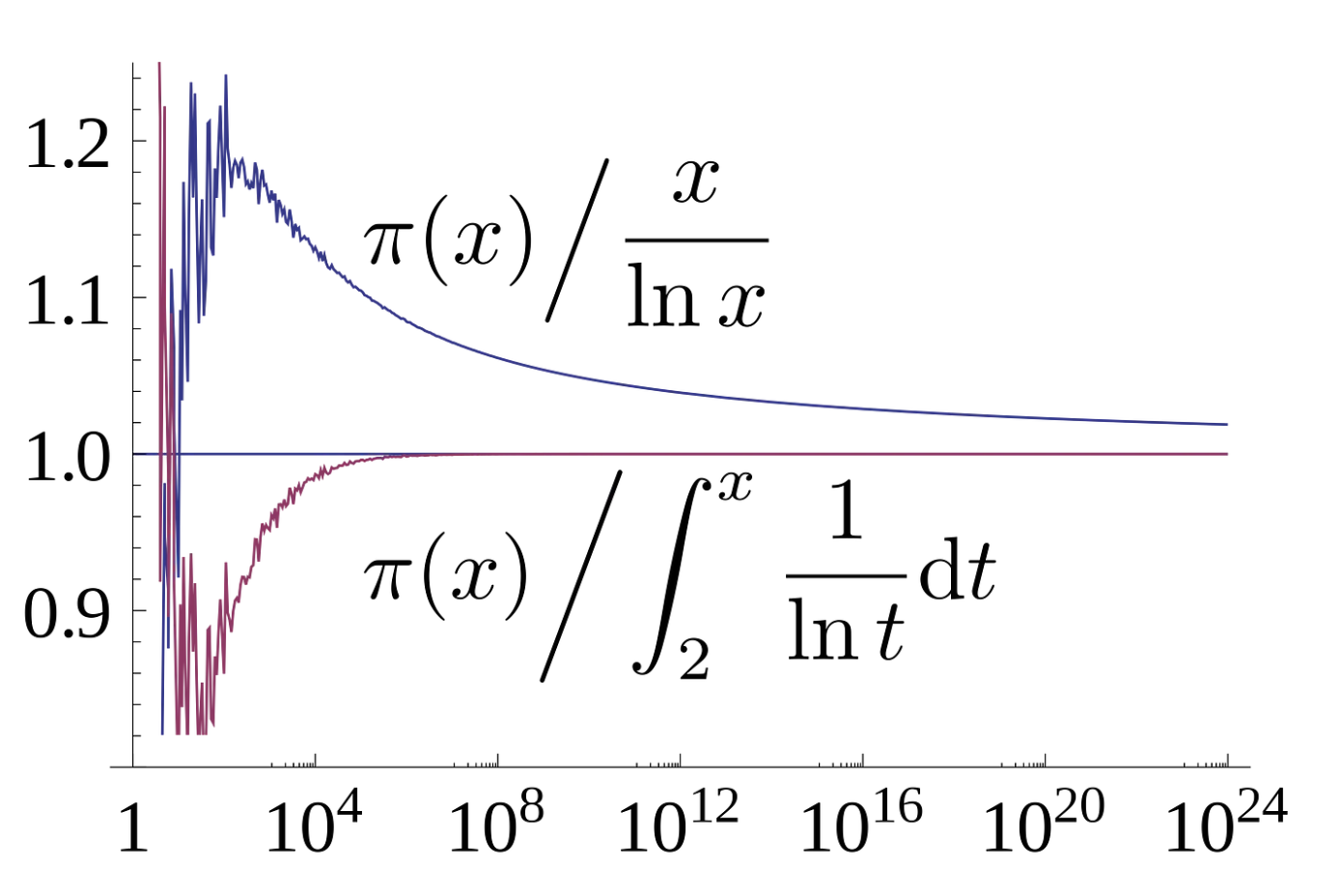 $\pi (x)$ limit as $x\rightarrow \infty$.
$\pi (x)$ limit as $x\rightarrow \infty$.
In the graph you can see how the count of prime numbers (the exact one) divided by the approximation tends to 1 for large x for the two approximations, the quotient and the integral. Actually the best approximation is the integral one. This result is very interesting and took many years to find, it gives some structure to this madness of prime numbers. But still, we can’t predict them and this is good for crypto!.
Primality testing and prime generation
In this section we investigate how to find prime numbers and test if an arbitrary number is prime.
A naive way to generate primes
The natural way to generate prime numbers is to start from the smallest one $2$ and test if the next one $3$ is divisible by $2$, since it is not, we add it to the list, then we have $2$, $3$. We go to test $4$ now, since it is divisible by one of the primes we already have $2$ we don’t add it to the list and we try the next one, $5$. $5$ is not divisible neither by $2$ nor by $3$ so we add it to the list, $2$, $3$, $5$ and so on… This is a very computationally intensive algorithm since all the time you have to check your full list that, by the way, is increasing every time you find a new prime.
The sieve of Eratosthenes
A faster way to generate prime numbers is using the sieve of Eratosthenes where basically you build a list of all the natural numbers from $1$ to $n$ ($n$ is the natural number below which you want all the primes) and remove all the multiples of the newly find prime. Say we want the prime numbers smaller than $n$=120. The algorithm starts with $2$, then you discard its multiples $2$, $4$, $8$, $\cdots$, $120$), you go for $3$ and you know it is prime because it hasn’t been discarded, so you eliminate multiples of $3$ that haven’t been discarded $3$, $9$, $12$, $15$, $\cdots$. The next number is $4$ and has been discarded so you go to 5 and add it as prime, then eliminate its multiples… You can find a nice implementation in python here.
Primality testing and Miller-Rabin algorithm
All the approaches so far seem to be very lengthly… in cryptography you often work with $256$ bit prime numbers ($2^{255}$ to $2^{256}$). Now, you can’t generate all prime numbers up to $2^{256}$ and then choose one at random, for this you need to use a test of primality. Basically what you do is draw a random natural number and then check whether this number is prime or not.
So given a natural number $n$, how can you tell if $n$ is prime or not? Remember first Fermat’s little theorem: Let $p$ be a prime number and let $a$ be any integer then
\[a^{p-1}=1 \mod{p}\]We may use it to check if $n$ is prime. If we plug $n$ instead of $p$ to the above equation (taking for instance. $a=2$) and find that $a^{n-1}(\mod n)$ is $1$ then can we say that n is prime?. The answer is no, because Fermat’s little theorem just goes in one direction (we need to know for sure that $p$ is prime). It does however give a good indicative that maybe $n$ is prime. So what if we test many different $a$? If we find that the power is $1$ for all of them can we say that $n$ is prime? Unfortunately the answer is again no. There are in fact numbers known as Carmichael numbers that are composite and its powers $a^{n-1}$ are always $1$. A well known Carmichael number is $561=3·11·17$ and whose powers are
\[a^{560}=1 \mod{561}\]for all $a$ smaller than $561$.
Seems we are in a cul-de-sac situation… But hopefully we have the Miller-Rabin algorithm to help us. This test was developed by Miller in 1976 as full deterministic test but then modified by Rabin in 1980 to make it a probabilistic algorithm. In order to circumvent the Carmichael numbers let me make the following proposition: Let $p$ be a prime (different from 2) then we can write $p$ in the form of
\[p-1=2^kq\]where q is an odd number and k an integer. Now let a be any number not divisible by p. Then one of the following two conditions is true
\[a^{q}-1=0 \mod{p}\]or
\[a^{cq}+1=0 \mod{p}\]for $c$ in $1$, $2$, $4$, $\cdots$, $2^k$. You can find the proof of this proposition is the book of Hoffstein, Pipher and Silverman. This happens strictly when $p$ is prime but let’s substitute this $p$ for an arbitrary number $n$. We can write $n-1=2^kq$ and find $a$ such that both conditions above are not fulfilled, then we call a a Miller-Rabin witness for the compositeness of $n$. I.e. if we find such a we know for sure that $n$ is composite.
Ok, but how many random $a$’s should one test to give a certainty of say 99% that the number $p$ is probably prime?. There’s another proposition that assesses that. Let $n$ be an odd composite number, then at least 75% of the numbers between $1$ and $n-1$ are Miller-Rabin witnesses for $n$. This means that if we randomly sample $10$ distinct values of a in the range of $1$ to $n-1$, the probability of hitting at least $1$ witness is $1- P(k=1, n=10)$=$0.99997$ (where $P$ is the Bernoulli probability). We are therefore quite sure that if with $10$ trials we haven’t found a witness the number is prime but we will never be 100% sure.
My implementation in code of the Miller-Rabin algorithm can be found here. Also the code to generate random prime numbers. Checking the calculation time with a regular laptop (2.6GHz 6 core 16 GB RAM) I get in between $25ms$ to $60ms$ to generate a $256$ bit random prime, in between $80$ and $120ms$ for $512$ bit prime and between $500ms$ to $2.15s$ for $1024$ bit prime. All this checking for $40$ maximum values of potential witnesses $a$.
Conclusions
Prime numbers are the building blocks of arithmetics and are very useful in cryptography. We’ve seen how prime numbers distribute in density, how to efficiently find them and how to test if a number is prime or composite using the Miller-Rabin primality testing.
Thank you for reading!.